写cesium快半年了,由于之前完全没没有接触过三维,而且很多概念也不清楚需要逐个去看文档理解,写的很吃力。今天把常用的计算转换做个总结,虽然文档里也有,但毕竟英文,搜索查找不便。
左右手坐标系:
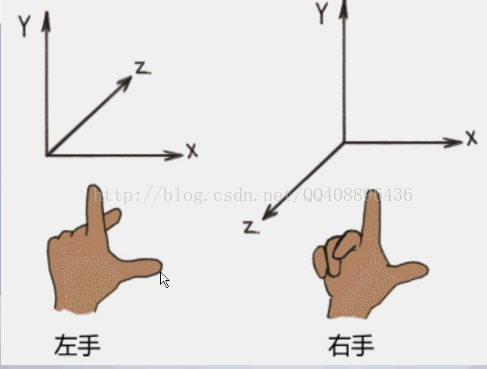
向量运算基础
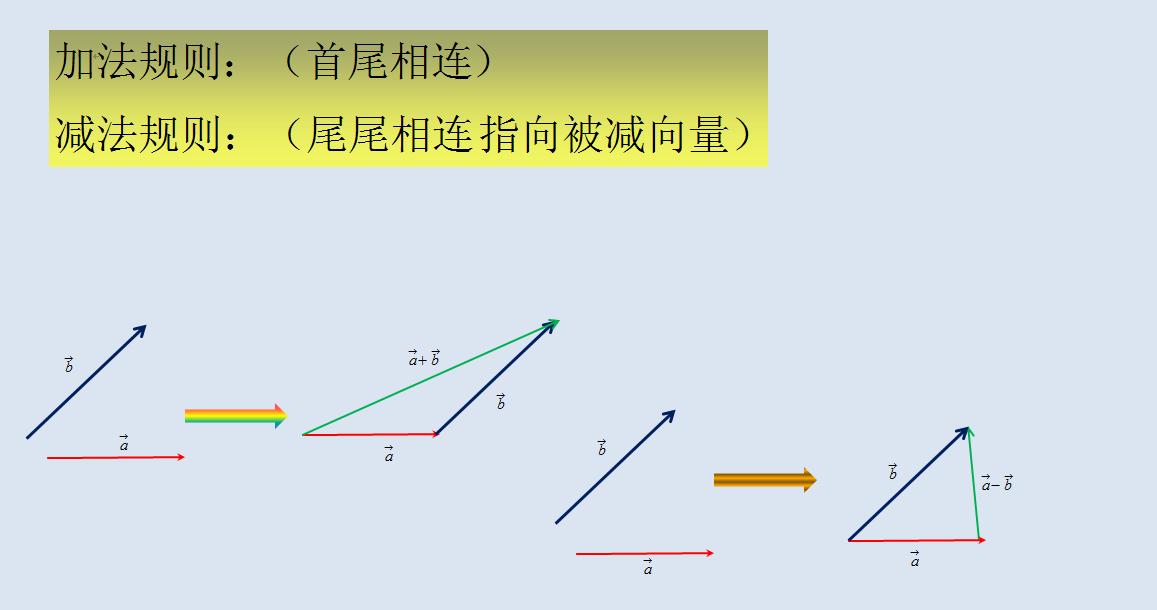
详见:
- 向量的概念、加减、数乘 – 知乎 https://zhuanlan.zhihu.com/p/428112596
1、空间坐标(笛卡尔坐标)转经纬度坐标(WGS84坐标)
Cesium.Cartographic.fromCartesian(cartesian);
由于Cesium.Cartographic的单位是弧度,可以使用Cesium.Math.toDegrees将其转为角度:
/**
* 笛卡尔坐标转经纬度坐标
* @param {Cesium.Cartesian3}
* */
export const cartesianToWGS84 = (cartesian) => {
const cartographic = Cesium.Cartographic.fromCartesian(cartesian);
const lat = Cesium.Math.toDegrees(cartographic.latitude);
const lon = Cesium.Math.toDegrees(cartographic.longitude);
const height = cartographic.height;
return { lon, lat, height };
}反向(经纬度转笛卡尔坐标):
//方法一
Cesium.Cartesian3.fromDegrees(longitude, latitude, height, Cesium.Ellipsoid.WGS84, result)
//方法二
var ellipsoid=viewer.scene.globe.ellipsoid;
var cartographic=Cesium.Cartographic.fromDegrees(lng,lat,alt);
var cartesian3=ellipsoid.cartographicToCartesian(cartographic);2、根据世界坐标求矩阵(该位置到局部坐标的变换矩阵)
世界坐标到局部坐标的变换矩阵,在很多场景都会用到
// 世界坐标到局部坐标的变换矩阵
const transformMatrix4 = Cesium.Transforms.eastNorthUpToFixedFrame(position, Cesium.Ellipsoid.WGS84, new Cesium.Matrix4());3、通过模型矩阵求位置、旋转角
位置:
const position = Cesium.Matrix4.getTranslation(modelMatrix, new Cesium.Cartesian3());旋转角:
const matrix3 = Cesium.Matrix4.getRotation(modelMatrix, new Cesium.Matrix3());
const quaternion = Cesium.Quaternion.fromRotationMatrix(matrix3, new Cesium.Quaternion());
const hpr = Cesium.HeadingPitchRoll.fromQuaternion(quaternion, new Cesium.HeadingPitchRoll());
// x: Cesium.Math.toDegrees(hpr.roll),
// y: Cesium.Math.toDegrees(hpr.pitch),
// z: Cesium.Math.toDegrees(hpr.heading)4、通过平移/旋转角求平移矩阵/旋转矩阵
平移:
// 从startCart3平移到endCart3的矩阵
const cartesian = Cesium.Cartesian3.subtract(startCart3, endCart3, new Cesium.Cartesian3());
const matrix4 = Cesium.Matrix4.fromTranslation(cartesian , new Cesium.Matrix4());旋转:
// 单分量,angle为弧度
cosnt matrix3 = Cesium.Matrix3.fromRotationX(angle);
// cosnt matrix3 = Cesium.Matrix3.fromRotationY(angle);
// cosnt matrix3 = Cesium.Matrix3.fromRotationZ(angle);
const matrix4 = Cesium.Matrix4.fromRotationTranslation(matrix3);
// 同时设置xyz分量,angleX|Y|Z为弧度
const matrix3 = Cesium.Matrix3.fromHeadingPitchRoll(
new Cesium.HeadingPitchRoll(
angleZ,
angleY,
angleX,
)
);
const matrix4 = Cesium.Matrix4.fromRotationTranslation(matrix3);多说一点:
先记录到这,后面再补充。